Fractional indices

The idea of building an algorithm

Indeed, the concept of fractional indexing presents a straightforward solution to our sorting challenge, akin to how one might intuitively approach the task on paper. For instance, envision writing down a list of items, and realizing the need to insert an additional item between two existing ones. Instead of renumbering the entire sequence, you simply designate the new item with a fractional index, such as 1.5.

While this intuitive approach forms the basis of fractional indexing, its direct application is hindered by the limitations of floating-point number representation. Floating-point numbers have finite precision, restricting our ability to split them indefinitely without encountering accuracy constraints.

To refine this concept, we introduce the notion of unattainable boundaries within the index range. Here, we designate zero as the unattainable upper bound and one as the unattainable lower bound, assuming rows are sorted in ascending index order.

Consider the scenario of inserting a row into an empty list: By utilizing these unattainable boundaries, we calculate the index as the midpoint between them, yielding (0+1)/2=0.5. Similarly, when inserting a row above an existing one, the new index is computed as the midpoint between the unattainable upper bound and the index of the previous row, resulting in (0+0.5)/2=0.25. Inserting between existing rows involves calculating the average of their indices, yielding (0.25+0.5)/2=0.375 in this case.

Upon closer examination of the resulting indices, we observe that the initial “zero-dot” prefix is common to all indices and can be disregarded. Furthermore, representing the index tails as strings or byte arrays facilitates lexicographic sorting, preserving the order of indices. This flexibility allows us to extend beyond numerical indices, incorporating characters from sets like base64 or even arbitrary bytes, provided our application or database supports lexicographic sorting of such arrays.

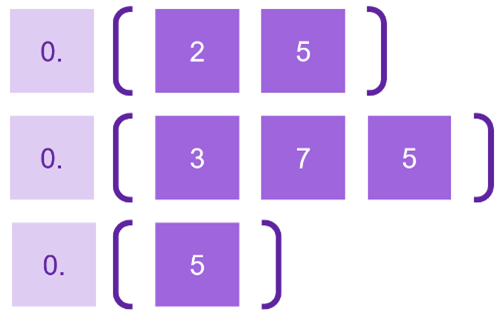
Insertion between indices

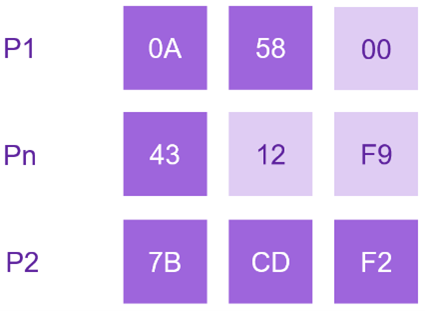
How to calculate a new index value between two existing ones?

To determine a new index value situated between two given indices, let’s take the byte arrays P1=[0A 58] and P2=[7B CD F2] as examples. Our approach leverages the concept of rational numbers, where trailing zeros don’t affect the value. E.g. 0.1 and 0.100 are the same number. This allows us to adjust the lengths of the indices by adding zeros as necessary.

Aligning the lengths of arrays is essentially multiplying our rational numbers by some common base so that they become integers. By treating these length-aligned indices as large integers, we can ascertain their arithmetic mean:

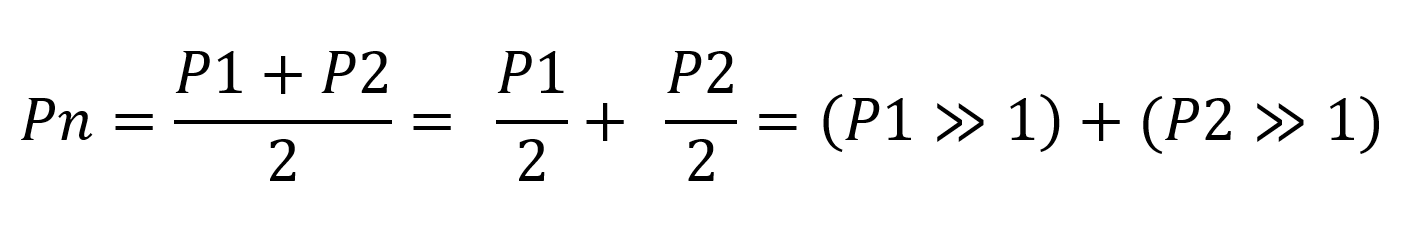
As evident from the aforementioned formula, achieving this merely requires executing two straightforward operations on arrays of bytes: Addition and right shifting by one bit. Both operations can be easily implemented for an arbitrary set of bytes. To do this, you just need to perform the operation on a pair of bytes and carry the remainder to the next one. Importantly, it’s unnecessary to retain all resulting numbers. Once a byte that differs between P1 and P2 is encountered, subsequent bytes become insignificant and can be discarded.

For instance, employing this method in our example yields the new index:

 

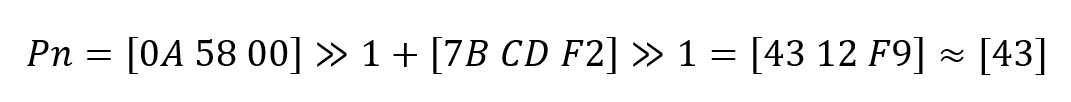
Memory estimation

The algorithm’s worst-case scenario occurs when continuously inserting new rows in the same position. With each insertion, the index range narrows, leading to a lengthening of the index. But how rapidly does this growth occur?

By implementing the algorithm with byte arrays and conducting 10,000 insertions at the list’s outset, we observe that the maximum index size reaches 1250 bytes. Thus, each insertion augments the index length by merely one bit.

This outcome is commendable, as one bit represents the minimum information size and appears difficult to improve upon. In fact, almost all descriptions of the algorithm stop there. However, it’s important to address edge cases separately, particularly insertions at the list’s very beginning or end. In these instances, a single open boundary exists, presenting an opportunity for optimization.

For example, consider a peer-to-peer text editor like Notepad, but the rows are sorted by fractional index. Every time we add a new row, our index increases by one bit. If you insert a line in the middle, nothing can be done about it. But when writing text, adding lines at the very end may be a more likely and natural way. Thus, by optimizing adding a new index to the end of the list, we can reduce storage overhead.

Memory estimation

Consider a straightforward scenario where the final index in our list is denoted as P1=[80 AB], and we aim to generate a subsequent index, Pn. Employing the preceding algorithm, we derive the new index value as Pn=[C0]. However, upon inspection, this increment appears too substantial. Instead, a more nuanced approach is warranted: Simply incrementing the first byte by one suffices.

Given that the initial index is precisely in the middle of the range, this observation facilitates approximately 127 insertions at the list’s end (or beginning) per first byte of the index. This equates to an approximate increase of 0.06 bits per insertion.

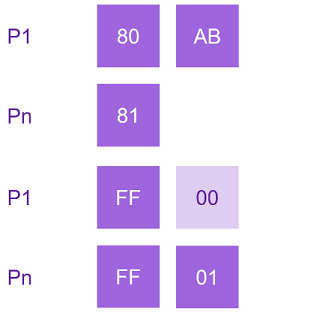
Moreover, leveraging the property of rational numbers, subsequent bytes are zero, enabling an additional 255 insertions per index byte. Consequently, this translates to roughly 0.03 bits per insertion.

An essential aspect of this algorithm modification is the incrementation of the index by one byte solely when reaching the edge values of the byte (FF for insertion at the end or 00 for insertion at the beginning of the list). As a result, the infrequency of reaching extreme values reduces the occurrence of new bytes.

By utilizing byte pairs for incrementation, efficiency is significantly heightened. This approach achieves remarkable values of 0.0001 bits for each new index. In such cases, identifying the first byte, excluding edge values, becomes pivotal, followed by incrementing the subsequent byte.

 

In essence, edge cases can be more efficiently managed compared to the basic algorithm. However, this optimization comes at the expense of the initial bytes of the index.

For our Notepad example, this means that indices will only grow by one bit when inserting into the middle of text, but adding lines to the end will cost relatively next to nothing.

Another example where this approach can work well is some kind of task or priority list application. Imagine a list with three tasks you constantly reorder in random order. Without optimization each move costs you a one bit in index. But the list has only three tasks, so the probability that we move task to very beginning or end is quite big. And this optimized case will trim the index back to initial bytes size.

 

Concurrency

Another aspect worth addressing is the concurrent editing of the list by multiple users simultaneously. What happens if two independent clients attempt to insert a row in the same location at the same time?

Let’s illustrate this scenario with a simple example involving two lines:

P1=[05 12] and P2=[07 0A]. Let’s assume two clients endeavor to insert a new line between P1 and P2.

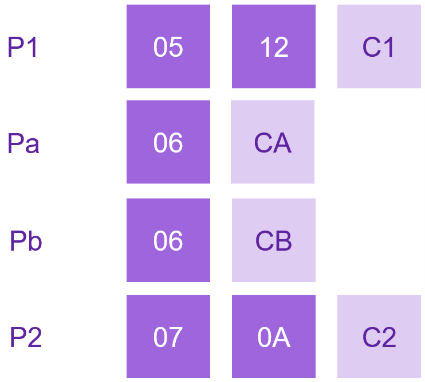
According to our algorithm, given the identical input data, both clients will obtain the same values for the inserted indices: Pa=Pb=[06]. This poses two significant issues. First, it leads to an undefined row order since the indices are identical, making it impossible to determine which should be higher. Second, and more crucially, the identical indices render us unable to insert anything between them.

To address this challenge, it’s imperative to ensure that the generated indices are unique. Here, we leverage a key characteristic of our indices: If we possess a list of unique values, appending any suffix to any index will not alter the row order. Consequently, we can introduce small, unique deviations for each client, guaranteeing the uniqueness of the generated values.

Such unique suffixes can be generated either each time a record is created or once at the application’s inception. The length of these suffixes can vary, balancing the likelihood of random collision with the additional memory required.

For example, in one of my pet projects I implemented the generation of a unique suffix 6 bytes long, according to the following rules:

The first two bits are constant zero-one. It is needed to break degenerate cases when the suffix consists of all zeros or ones. Since we know that such suffixes can have a significant impact on the length of the index at the beginning or end of the list.

The next 21 bits are random. This order allows us to reduce the expected length of the index so there is less chance of identical bytes, and we can truncate the index earlier when inserting a row between two existing ones.

And the last 25 bits are the truncated Unix time stamp. This is an annual cycle, but it allows us to significantly reduce the likelihood of generating duplicate suffixes because the calculation is done once at application startup.

Conclusion

In summary, we have successfully developed an algorithm that efficiently sorts records with minimal list alterations. By addressing challenges such as concurrent client operations, we have enhanced the algorithm’s flexibility and efficiency. Notably, we have optimized insertion cases at the list’s beginning or end, ensuring robust performance across various scenarios.

References

https://www.figma.com/blog/realtime-editing-of-ordered-sequences/